|
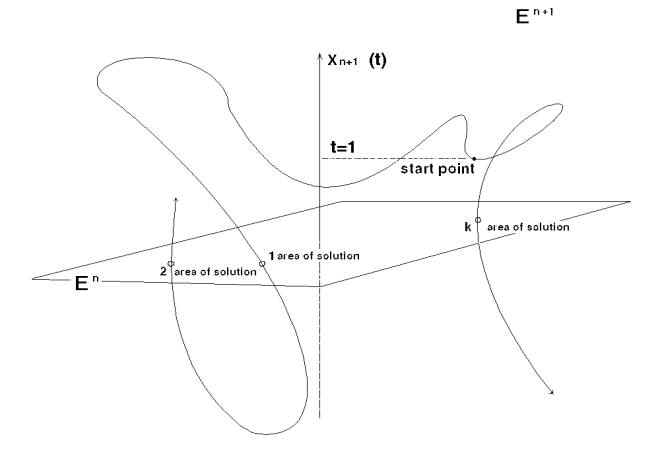
l | Now, accepting a length of arc of this curve as an independent parameter we can move in space |
| along this curve in both directions from a selected point and follow the change of the sign of t | |
| (first moving from the selected point with a step with a sign “plus” and then moving with a step | |
| with a sign “minus“ (or vice versa). And when the curve is intersecting space |
| n | |
| E |
| we fix an area of solution for (1). Thus the roots considerably removed from the start point can be |
| found, and the amount of solutions found for one start point can be more than 1. |

This way allows us to move along greatly oscillating curve and to pass points of self-intersection. |
| For a further improvement of the found roots we can use this method or any of |
| wellknown ones - in particular, we can use the Newton's method. |
There is a theorem demonstrating that the Newton's method is a special case of our method in such a case where the Euler's method is used to solve the system of the differential equations with a parameter's step equal to 1.
|
|